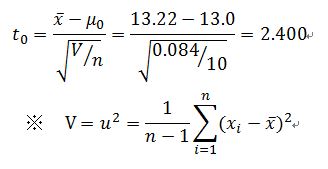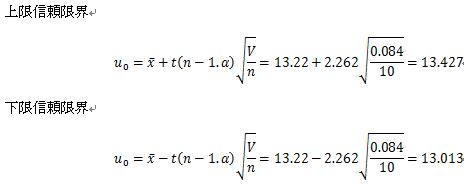検定・推定とは?
工程中で治具改善をしたり、材料改善をしたりした際、改善前と改善後のデータを比べ評価します。
その中で、「どのような分布だったらよくなったと言えるのか?」というのは、評価で悩むところの1つです。
それを統計的に処理する方法として、検定・推定という計算方法があるので、紹介します。
「推定」
・無作為にとった一部のデータから、全体の平均(もしくは分散)がどの範囲に入るかを推定することです
・これから起こりうるデータに関して「◯◯から△△の間に95%のデータが収まる」ということが言えます。
「有意水準5%(信頼区間95%)」
有意水準95%=もし100回同じような推定を行ったとすれば、そのうち95回は、平均が○~○の間に入ると推定されるという意味です。
「検定」
・「この値は推定結果から普通の値といえる(もしくは普通の値といえない)」かどうかを検定することです。
・主張したい仮説(対立仮説。例:「工程改善後の強度が良くなっている」)に対して、主張したいものと逆の仮説(帰無仮説。例:工程改善前後の強度は同じである」)がどのくらいの確率で成り立つのか計算し、その確率が非常に小さい(5%以下)ならば、主張したい仮説が成り立つといえます。
(例題)
ある丸棒を仕様により15~20mmの長さに切断する工程がある。
装置を変更し、13mmの長さになるように調整した。
結果として下記の10個のデータを測定したが、正しく調節されているといえるか?
13.0 13.8 13.2 13.2 12.7 13.4 13.1 13.3 13.4 13.1
(手順1) 帰無仮説
H0と対立仮説
H1、有意水準
αを決定します
H0:μ=μ
0 (=13.0) ※「工程改善後の寸法が13mmである」という仮説
H1:μ≠μ
0 ※「工程改善後の寸法が13mmでない」という仮説
α:0.05
μ:工程改善後の母平均(=サンプル以外も含めた工程全体の平均)
μ
0 :期待する母平均(=サンプル以外も含めた工程全体の平均)
α:有意水準(何%以下でμ
0が成り立つなら非常に確率が小さいとするか)
※このα:有意水準については、計算する人が設定する必要があります。仮説検定において、仮説が真でにもかかわらず、これを偽りであるとして棄却し、対立する仮説をとってしまうという誤りを犯す確率のことです(第1種の過誤といいます)。通常1~5%のことが多いです。
(手順2)検定統計量を求める
※検定推定量…母集団においてt分布という分布が成り立つとしたときの関数
※t分布…正規分布する母集団の平均と分散が未知であり、標本サイズ(サンプリング数)が小さい場合に平均を推定したいときに利用される確率分布
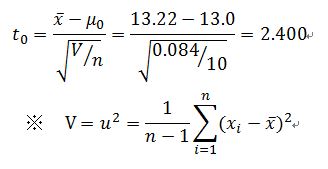
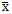
:標本平均(サンプル10個の平均)
V:標本分散(サンプル10個の分散)
※今回は母集団の平均が未知のため、普遍標本分散u
2を使用し、平均からの差の二乗和を(n-1)で割っています。サンプリングして分散を計算する場合、母集団の分散より小さくなるため、分散を大きめに見積もる意味合いがあります。
(手順3)検定
|t
0|≧t(n-1, α)ならば有意で、H
1「工程改善後の寸法が13mmでない」という証明となります。逆に、有意でないならば、H
1の仮説を棄却できます。
(言い換えれば、
H0:「工程改善後の寸法が13mmである」という仮説が成り立つ確率が5%以下かどうかの検定ということです)
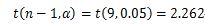
t(n-1, α):サンプルn個のときのt分布の関数値(関数表より)
※上記はt分布の数値表より。意味合いとしては、データ分布の右側2.5%+左側2.5%以上の、中央から外れたデータは|t
0|という数値で表すといくつ以上か?ということです。つまりこの場合は、計算して出した|t
0|の数値が2.262以上の数値の場合は、
H0:「工程改善後の寸法が13mmである」という仮説が成り立つ確率が5%以下ということになります。
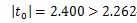
よって、(手順2)で計算した通り、
H0:「工程改善後の寸法が13mmである」の成り立つ確率は5%以下と言えるため、
H0は棄却されます。
データだけ見ると13mmに調節されているように見えてしまうのですが、有意水準5%(信頼率95%)の計算条件において、正しく調節されているとはいえないということになります。
では、実際にはこの工程変更後の分布はどうなっているのかを推定します。
信頼係数95%の信頼限界は、下記の式で計算できます。
※信頼係数…信頼区間の当たる確率。
※信頼限界…もし100回同じような推定をしたときに、その内95回は平均がこの信頼区間内に入ると推定されます。
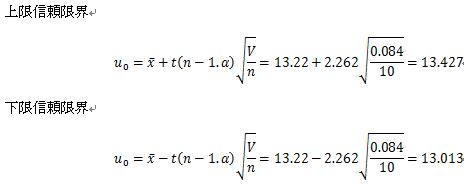
この計算結果から、もし100回同じような推定を行ったとすれば、そのうち95回は、平均が13.013~13.427の間に入ると推定されるといえます。