ものづくりを楽しむ社員がリレー形式で更新します。
筆者は、ピンクの夫婦が住んでいることと、朝から飲み屋が空いていることで有名な東京最北端の街に住んでいます。
家は駅から歩いて20分強の昔ながらの住宅街にあるのですが、家の周辺の道は幅がとても狭いのが難点。
車が通ることを想定していなかった時代の名残で、乗用車一台がギリギリ通れるくらいの幅しかないところがたくさんあります。
よく見るサイズの消防車は絶対に通れない幅なので、火事が起きたときはヤバイこと請け合いです。
私はそんな細い道を通って駐車場に車を入れています。（しかもバック(>_<) ）
左右の壁までほとんど隙間が無い状態で進めなければならず、
最後の数十メートルが毎度の神経すり減らしポイントです。
仮に車の幅をサイドミラー含めて2メートル、道幅を2.5メートルとしましょう。
平日はその道を歩いて通るのですが、人通りはほとんどなく、
道の真ん中を歩いているため、壁にぶつかる危険性などまず感じません。
ここまでの話を画にすると以下のようになります。
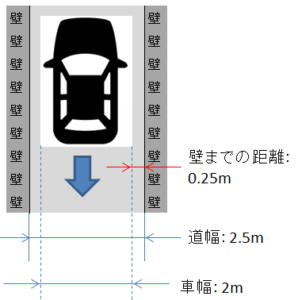
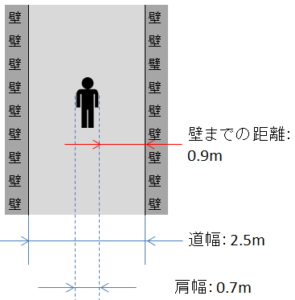
壁にぶつかる「ヒヤヒヤ度」は圧倒的に 車 ＞ 徒歩 です
徒歩の場合でも、自転車が来て脇に寄った場合、壁に近くなりますので、「ヒヤヒヤ度」は高くなります。
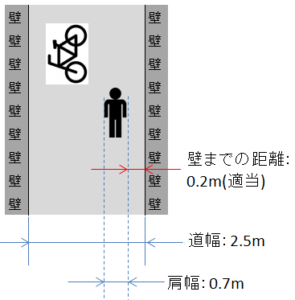
お察しの通り、このヒヤヒヤ度を数値化した物がCpK。。。
と言いたいところですが、CpKにたどり着くにはもう少し知っておかなければならないことがあります。
それは「ばらつき」。
今回はよくみかける左右対称のグラフをベースに話を進めます。
(正規分布と呼ばれる分布のグラフですが、詳しくはWEBで！！)
1000人の学生がテストをうけ、平均点が50点だったと仮定しましょう。
50点を取った学生が一番多く、60点、70点、80点と点数が高くなるほど該当の学生数は少なくなります。
40点、30点、20点と低い方も同様です。
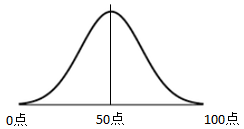
ここで「ばらつき」を数値化してわかりやすくするために、「標準偏差」という値を計算します。
ややこしい感じもしますが、「平均値からの差の平均値」です。
60点と平均点(50点)の差は10点、30点と平均点(50点)の差は20点、・・・
という風に平均点との差を1000人分足して、それを1000で割った数です。
※一般的には”((値-平均)２の累計/データ数)の正の平方根”が「標準偏差」を求める式
マイナスの数値を無くすために2乗してもとに戻すために平方根を取るという
計算が含まれているので、ちょっと複雑。
「標準偏差」はシグマとも呼ばれ、σという記号で表わされます。
正規分布のグラフと標準偏差の関係性は以下の通り
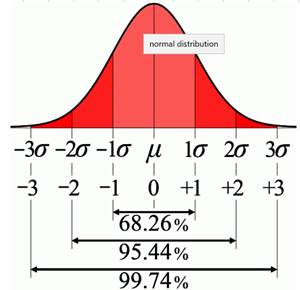
上のテストの例で標準偏差が15点だった場合、
平均点50点の前後1σ(+15点と-15点 = 35点～65点の間)に68.26%、
1000人中680人くらいはこの範囲の中にいるということになります。
同様に、平均点50点の前後2σ(+30点と-30点 = 20点～80点の間)なら95.44% =約950人
3σの場合5点～95点の間に99.74% =約997人ということなので、100点満点を取った人、
もしくは0点だった人はそれぞれ一人いるかどうかという分布になります。
平均からプラスの方向に3σ、マイナスの方にも3σ、
合わせて6σの範囲で99.74%がカバーされるので、ほとんど皆この範囲に収まるということですね。
ここで話はヒヤヒヤ度に戻ります。
最初に示した図の車や人をばらつきのグラフに置き換えてみます。
図1:車 図2：徒歩
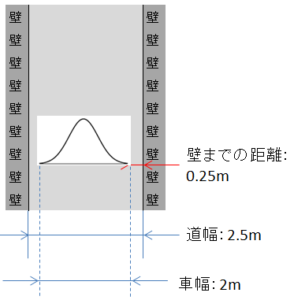
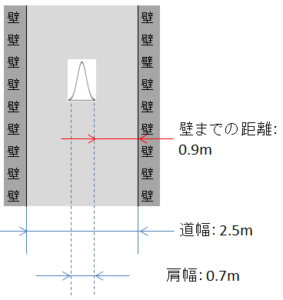
図3：脇に寄った場合
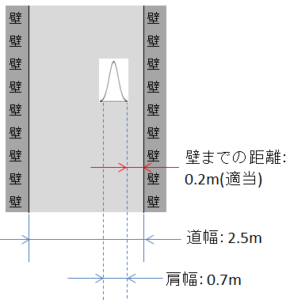
壁にぶつかってしまったらアウトなので、左右の壁を上限値と下限値に置き換えてみます。
（製造工場ではこの値を超えたらNG品ということになります。車なら事故。）
図1:車 図2：徒歩
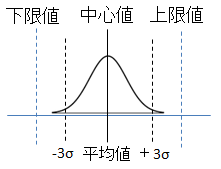
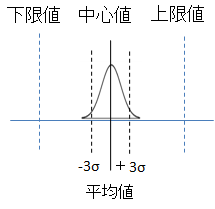
図3：脇に寄った場合
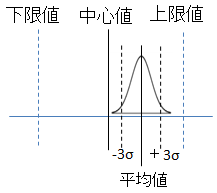
CpKの計算式ですが、 (上限値-平均値)÷3σ と (平均値-下限値)÷3σ の
小さい方の値という定義になっています。右か左か、壁に近い方を見たときのヒヤヒヤ度ということです。
車が道のど真ん中にあったとしたら左右の壁までの距離は同じなので、
左右どちらの壁を見てもヒヤヒヤ度は同じ。
言い換えると、
中心値と平均値が一致していた場合、平均値から上下限値への距離はどちらも同じなので、
上限値と下限値どちらの値を使って計算してもCpKは同じです。
同じど真ん中でも、壁までの距離に違いがあるので、
車と徒歩ではヒヤヒヤ度が異なります＝CpKが異なります。
上に載せた図で見ると、車の図の場合、平均値と上限値の間に入る3σは1.5個分くらいでしょうか。
それに対して、徒歩の方は3σが4つ分くらい入りそうです。
徒歩でも自転車が来たため脇に寄った場合、3σが2つ分くらいに減ります。
これら1.5、4、2というのがCpKになります。
数値が低いほどヒヤヒヤ度が高く、数値が高いほど安心度が高いということになります。
工場での生産に当てはめると、CpKが低いほど工程が安定しておらず（NGが出る可能性が高い）、
CpKが高いほど工程が安定している（NGが出にくい）ということになります。
だからCpKは日本語だと工程能力指数って言うんですね。
製造工場ならCpkは最低でも1、出来れば1.33以上欲しいと言われるので、
上の例だと車でも全然大丈夫ということになりますが、あくまで例なので、あしからず。
ちなみに、まだ壁に擦ったことはないので、私の運転技術のCpKは1以上かな。